Inseguimento fotografico di comete veloci

Un nuovo metodo per un inseguimento preciso nella fotografia cometaria.

Gianluca Li Causi

4 Aprile 1997

Le difficoltà nella fotografia di comete veloci

La fotografia delle comete richiede all’astrofotografo un notevole impegno nella guida al telescopio, principalmente per due motivi: 1) ci si trova a dover mantenere al centro del crocicchio di guida un oggetto tutt’altro che puntiforme, come la chioma di una cometa il cui falso nucleo spesso è mal definito; 2) il moto della cometa richiede interventi di correzione su entrambi gli assi della montatura, ascensione retta e declinazione, con una frequenza molto alta.

Le correzioni da eseguire dipendono dalla geometria dell’incontro tra la cometa e la Terra e sono maggiori nel periodo di massimo avvicinamento, quando la cometa puó arrivare a spostarsi in cielo anche di decine di gradi al giorno. Tale situazione si è presentata ad esempio durante il passaggio della cometa Hyakutake che, nella notte del suo massimo avvicinamento, il 25 marzo 1996, sfrecciava a ben 15 gradi al giorno con un’elevatissima inclinazione dell’orbita, puntando dritta verso il polo celeste e rendendo necessarie correzioni in declinazione ogni due secondi.

Nei prossimi mesi saranno visibili due comete molto luminose, la Q4 NEAT e la T7 LINEAR, che passeranno rispettivamente a circa 0.3 e 0.2 unitá astronomiche dalla Terra. La Q4 in particolare ha un’orbita molto inclinata in declinazione perciò ci dará problemi di guida analoghi alla Hyakutake, mentre l’effetto sará piú contenuto per la T7.

In casi come questi, se le dovute correzioni non vengono fatte con la massima attenzione, può accadere che le tracce stellari nella foto finale ne rivelino l’imprecisione mostrandosi di una forma a “zig‑zag” invece che rettilinea.

La soluzione

La soluzione ottimale consiste nell’uso di un circuito elettronico programmabile in grado di inseguire automaticamente la cometa in base alle effemeridi, ma questa possibilità non è solitamente disponibile nelle strumentazioni amatoriali.

La soluzione che proponiamo in questo articolo è di estrema semplicità e ugualmente efficace e si adatta bene alla strumentazione amatoriale senza la necessitá di alcuna elettronica aggiuntiva.

L'idea è la seguente: se puntassimo l’asse polare della montatura sul polo dell'orbita apparente della cometa, invece che sul Polo Celeste, potremmo inseguire la cometa con il solo motore di ascensione retta, senza alcuna correzione in declinazione (fig. 1).

La grande cometa Hyakutake
Fig. 1: Fotografia della cometa Hyakutake effettuata col metodo descritto nel testo (Obiettivo 180 mm F/4, posa 18 min su Ektar 1000)

L’orbita apparente della cometa rispetto all’osservatore è la composizione del moto di rotazione terrestre con il percorso della cometa rispetto alle stelle: essa quindi non è semplicemente un cerchio centrato sul Polo Celeste, come avviene per le stelle, ma è una curva più complessa di forma spiraleggiante. Se conoscessimo, in ogni istante, il centro di curvatura di questa traiettoria, vi potremmo puntare direttamente l’asse polare della montatura, cosí che il moto di inseguimento risulti automaticamente parallelo al movimento della cometa nel cielo. Basterebbe a quel punto regolare la sola velocità di inseguimento, o correggere solo in ascensione retta, per avere una guida perfetta. Dobbiamo solo calcolare le coordinate di questo centro per la data e l’ora della nostra osservazione: la sua posizione infatti non è fissa e per ogni fotografia bisognerà allinearsi su un punto leggermente diverso.

In questo articolo presentiamo i risultati di questo calcolo per le comete Q4 e T7. In figura 2 riportiamo la cartina stellare per il corretto posizionamento dell’asse polare per queste due comete: la mappa mostra la posizione del polo dell’orbita apparente tra le stelle intorno al Polo Celeste, calcolata per l’istante centrale di una posa di 15 minuti. Notiamo in particolare come, a ridosso del massimo avvicinamento, questo punto si allontani di quasi un grado dal Polo Celeste per la cometa Q4 e di meno di mezzo grado per la cometa T7. In quei periodi infatti le due comete saranno molto veloci e con una notevole componente in declinazione (soprattutto la Q4): questo vuol dire che con la guida usuale saranno richieste frequenti correzioni in declinazione, mentre, grazie al metodo che proponiamo, un semplicissimo spostamento dell’asse polare renderà la guida estremamente facile e precisa.

Per un allineamento ancora migliore il programma compila un tabella con le coordinate equatoriali del polo dell’orbita apparente calcolate, nel formato riportato come esempio in Tab. 1.

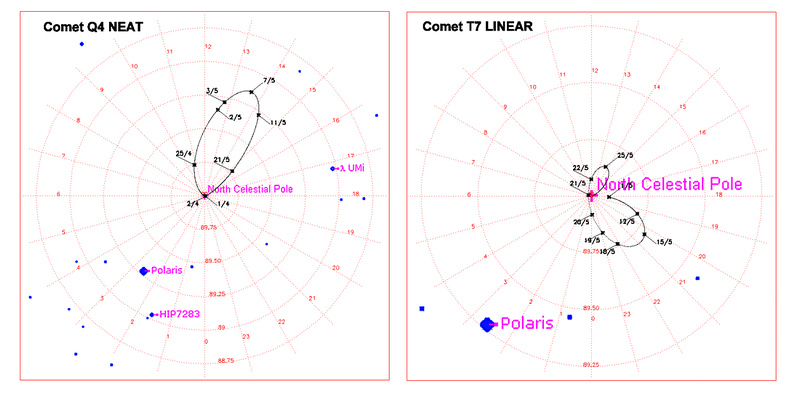
Fig. 2: Traiettorie del polo dell’orbita apparente per le comete Q4 NEAT e T7 LINEAR nei prossimi mesi, calcolate per una posa di 15 minuti. Le date riportate corrispondono alle 00:00 di Tempo Universale. L’asse polare della montatura deve essere puntato, prima di ogni foto, nel punto corrispondente alla data e all’ora corrente.

A questo punto un astrofilo esperto potrebbe obiettare che il disallineamento dell’asse polare della montatura dal Polo Celeste potrebbe provocare sulle foto il noto effetto della rotazione di campo, che consiste in una rotazione di tutta l’immagine attorno al punto di guida con la conseguenza di un “mosso” circolare sulla foto finale (è proprio per evitare questo effetto che si pone sempre molta cura nello stazionamento in Polare della montatura). Questo effetto può diventare molto fastidioso nelle foto fatte con pellicole ad alta risoluzione, come la TP2415, o in inquadrature di porzioni estreme della coda eseguite a lunga focale le quali, essendo lontane dal nucleo sul quale si guida, subirebbero un effetto di rotazione di campo maggiore, oppure può rovinare le pose molto lunghe che si rendono necessarie se si utilizzano i filtri di selezione cromatica, come il blu (Wratten 47B) che viene usato per isolare la coda di ioni (fig 3).

In figura 4 abbiamo quindi calcolato la rotazione di campo per una posa di 30 minuti con la montatura allineata sul polo apparente delle due comete. I grafici indicano la lunghezza del “mosso” all’angolo di una foto su pellicola 24x36 mm: se questo “mosso” è minore delle dimensioni della grana (che va dai 40 agli 80 micron a seconda della sensibilità della pellicola), la rotazione di campo è invisibile. La figura 4 ci assicura quindi che per queste due comete possiamo usare con tutto vantaggio il metodo proposto senza alcuna controindicazione.

Il programma, in linguaggio IDL, che esegue i calcoli mostrati è a disposizione dei lettori nel sito internet dell’autore (/www.notturni.it): il programma richiede la tabella con le effemeridi della cometa (pubblicate sul sito della NASA http://encke.jpl.nasa.gov/eph.html) e il tempo di esposizione previsto per la foto, in modo da considerare anche il movimento del polo apparente durante la posa stessa. Per chi non è digiuno di programmazione riportiamo nel riquadro le formule usate, con le quale non sarà difficile scrivere un proprio programma nel linguaggio preferito.

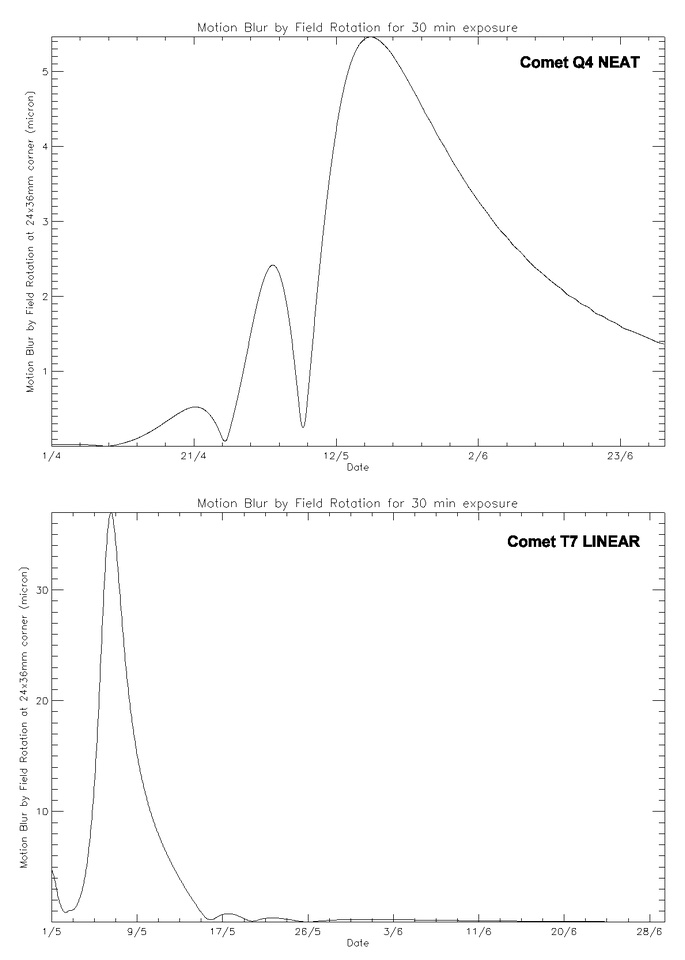
Fig. 4: Lunghezza del “mosso” dovuto alla rotazione di campo all’angolo del formato 24x36mm per le comete Q4 e T7. Si nota come per entrambe le comete il mosso sia minore di 40 micron e quindi paragonabile alle dimensioni della grana della pellicola.

APPENDICE: L'algoritmo di calcolo

Il software da scaricare

Il programma illustrato e' liberamente scaricabile dalla nostra pagina del software.